FSM - Functional State Machines

Plan?

In my previous F# Advent Calendar blogpost, Many faces of DDD Aggregates in F#, we explored a "tactical DDD" building block called Aggregate.

One of the solutions was something that I called functional, state machine-like approach.

In this tiny tale, we are going to explore state machines more.

Not just any state machines.

Functional ones.

What does this mean?

Functional, State Machine-like approach

Let's refer to a type descriptions of a finite state machine (FSM) that we saw in Functional, State Machine-like approach:

module StateMachines =
    type FSM<'Input, 'Output> = FSM of 'Output
    //          \______ used  mostly for documentation - what input is possible
    type Evolve<'Input, 'Output, 'FSM> = 'Input -> 'FSM -> 'Output * 'FSM
    type Aggregate<'Command, 'Event, 'State> = FSM<'Command, 'Event list * 'State>
    //                           'Input   ____________/                \________ 'Output with implicit state

It captures the story behind our intentions - Evolve<'Input, 'Output, 'FSM> function expresses what we can do with a finite state machine (FSM<'Input, 'Output>).

Imagine that we have a magical device that no one ever dreamed of - Func-o-meter.

Func-o-meter can measure and tell us how functional the given piece of code is.

A device for measuring functional levels of a given piece of code

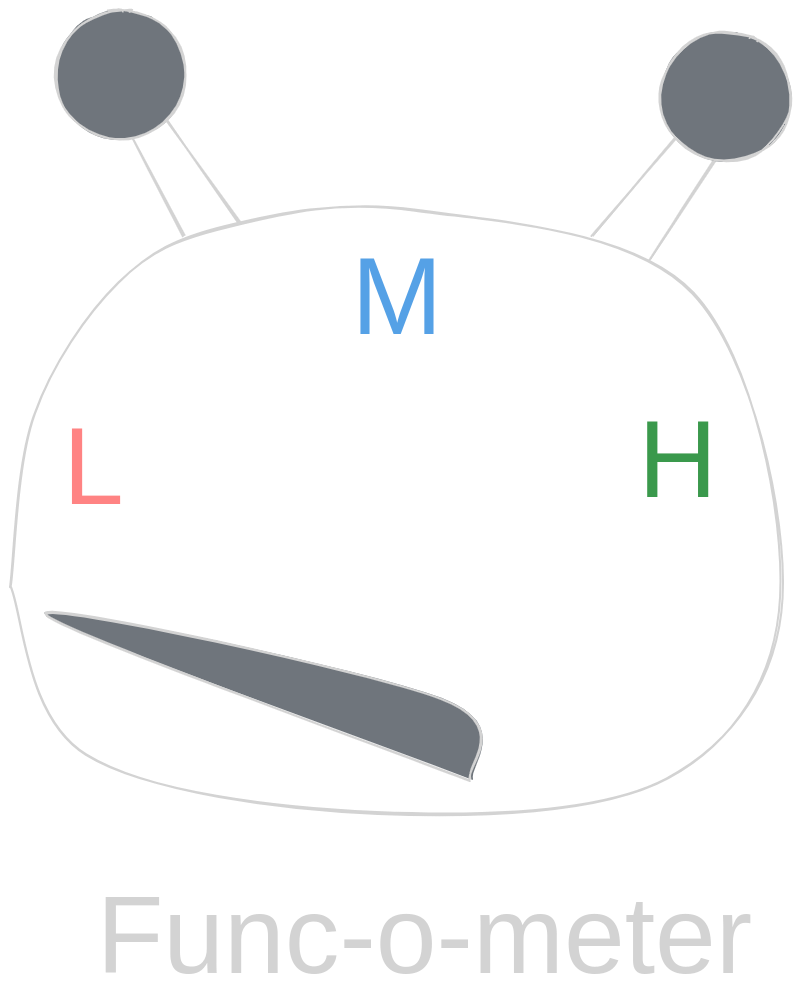
Regarding the symbols on the screen:

• L means Low
• M means Medium
• H means High

Sounds magical?

Good, because it is pure (pun intended) magic.

We just need to point at the code with those two strangely looking antennas and we can get the measurement result back.

The result you just saw, dear Reader, was me trying to use our Func-o-meter on Object-Oriented approach from previous tale.

Well, it's not that functional, isn't it?

Let's try to use Func-o-meter on our little snippet, presented just before.

Showing how much our FSM-like implementation is functional

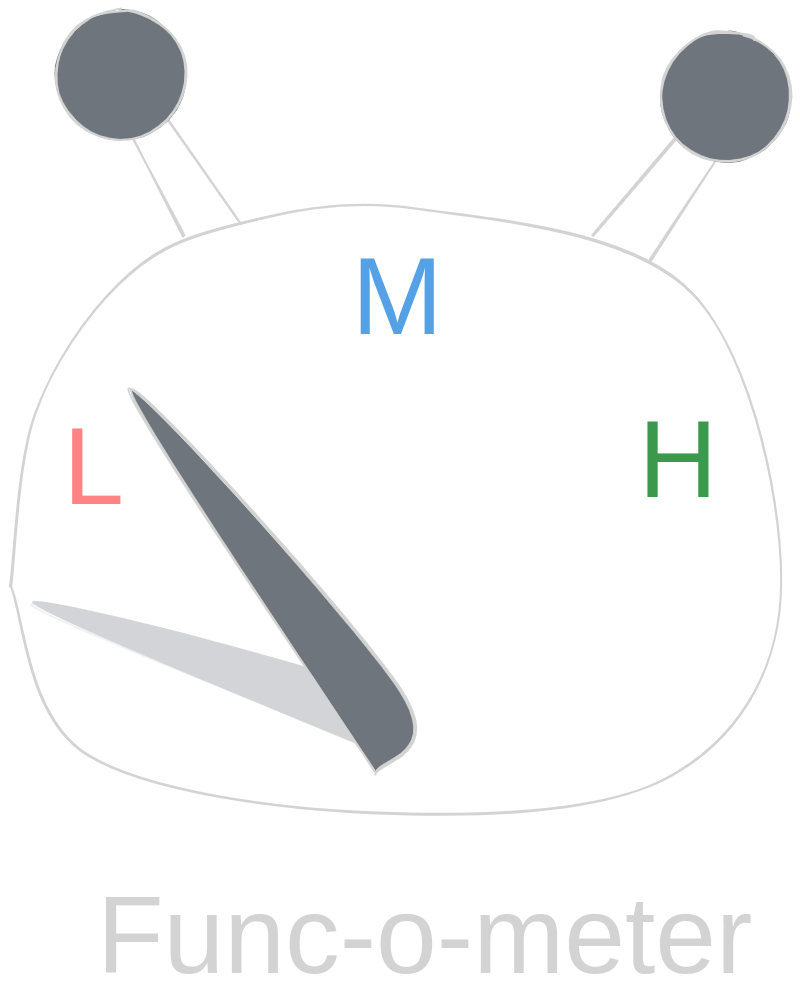
And here we are - it's pretty functional in comparison to OO one.

We are on the good path, aren't we?

Actually, it's really neat function (pun intended) of Func-o-meter - you are able to compare results of two consecutive measurements.

But wait, do you have any problem?

Problem?

Building something just to build something is really interesting idea, but no.

We need to have a goal.

A problem to solve.

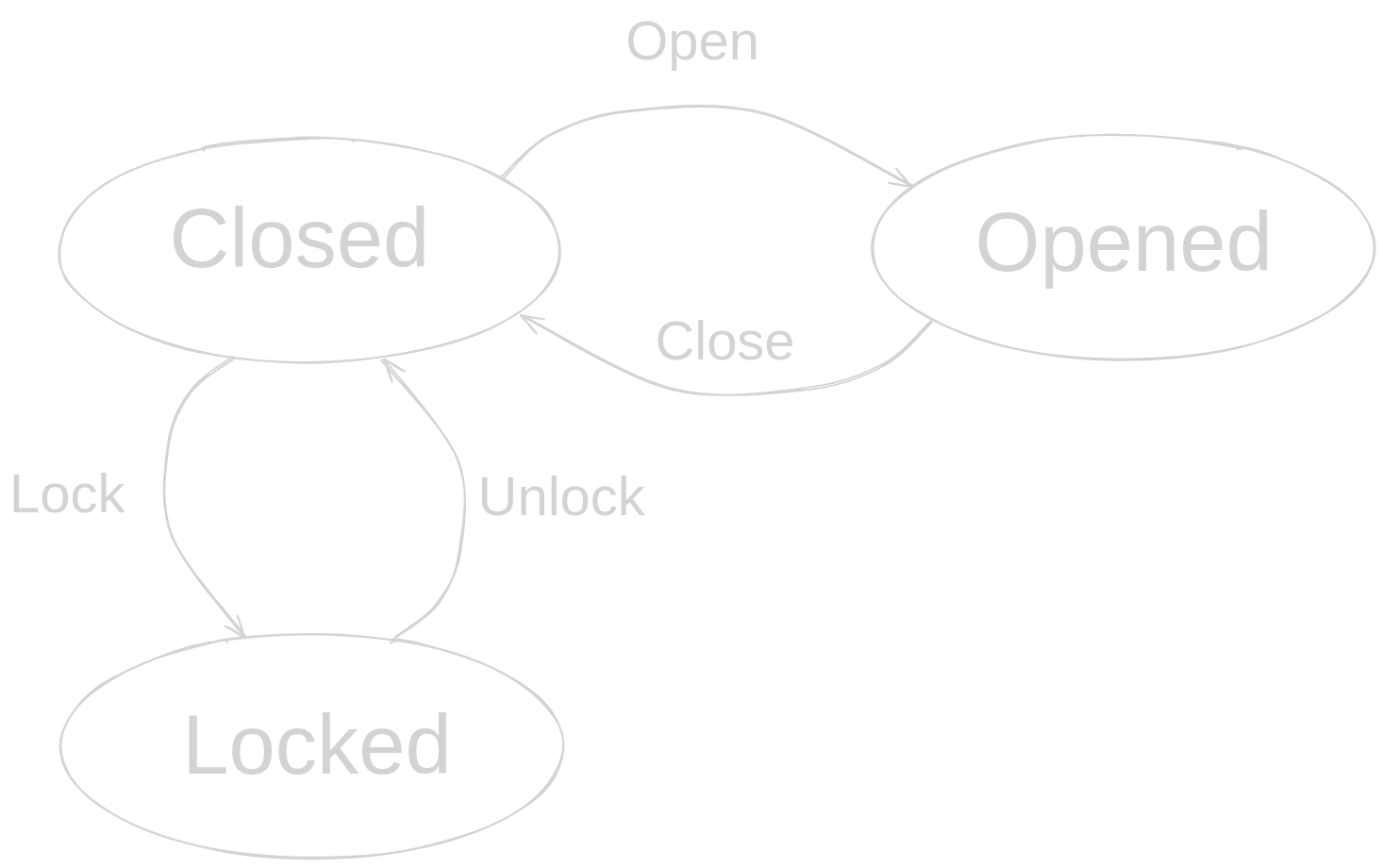
This time our "problem" is pretty straightforward - we are going to try to model door mechanism.

That mechanism can be either opened, or closed or locked.

As you probably can predict, dear Reader, only some actions are able to be applied to a door mechanism in a certain state.

We could conclude the rules in the following list:

• door mechanism starts as Closed
• only when it's Closed, when trying to Open it, it becomes Opened
• only when it's Opened, when trying to Close it, it becomes Closed
• only when it's Closed, when trying to Lock it, it becomes Locked
• only when it's Locked, when trying to Unlock it, it becomes Closed

If one could visualize it, it might look as follows:

A specification of how a door mechanism could work

Is it too naive example?

We need to have a simple problem to focus more on the modeling aspect.

Ok, fasten your seat belts, and let's start!

Solution #1: Mealy State Machines

Our first attempt, for gaining more functional points, will be by using Mealy machines.

As you probably know me a bit, dear Reader, I like to focus on language when modeling and solving problems.

Let's then use mathematical language and a bit of the theory to define a Mealy machine:

As we are diving into functional stuff, things must be mathematical in its purest form (as our functions, right?) - and also difficult.

Of course, I am joking.

We won't go into a theory that much.

Let's be pragmatic and focus on our goal - solving a real problem!

We could think of a Mealy finite state machine as such that its outputs are determined both by their current state and their current input.

A little computer that has some internal state and based on a given input, it change its internal state to one of finite states set.

We could represent it as follows:

type Mealy<'Input, 'Output> = 'Input -> 'Output * Mealy<'Input, 'Output>

So it basically gets input and does some magic to move to next state, based on some logic, and as an output it returns current state and itself.

But it's not really the same "self".

Our little machine got transformed by utilizing input and internal state - and we got "new existing" machine.

Immutability in its greatness.

No mutability, just transformation.

Turns out that it's a pretty well-known "problem" of representing Mealy state machines.

In one of my discussions with borar, he referred to purescript-machines.

It is a PureScript implementation of Mealy machines with halting.

Really briefly - halting means that that our machine can "stop" when reaching a termination state (it's on us when we define so).

I must admit it was a great resource to understand how to implement it correctly in F#.

With borar's help, it was even easier.

So let's introduce "stopping a machine" concept and Mealy finite state machine properly:

type Step<'Output, 'Continue> =
| Stop
| ContinueWith of ('Output * 'Continue)

type Mealy<'Input, 'Output> = 
    Mealy of ('Input -> Step<'Output, Mealy<'Input,'Output>>)
//       THIS IS OUR CONTINUATION! ______/

In order to utilize "stopping a machine", we need to introduce a concept of Step.

It represents intention of how state machine should behave.

The most interesting part is ContinueWith because it yields information about the output and a continuation.

Typically a continuation is a function that contains description of what needs to be done next.

And now we have our precious machinery - Mealy.

It keeps a function from an input to a step.

An avid Reader might notice that Step, as a second type parameter, uses a continuation.

In our example its another Mealy type...Which holds a function.

Isn't it weird? Shocking?

So our Mealy is keeping a function that produces a pair of output (from a state machine) and a Mealy, that keeps a function that produces a pair of...

...I hope you see where it goes.

We are going to create a recursive function there.

Isn' it too dangerous to build such recursive construct in that particular way?

Well, in case we couldn't stop it, it might be a bit interesting to see how stack is exploding.

But thanks to Stop case of a Step type, any time our state machine yields Stop - no more steps are possible.

But where were we - we have the problem to solve!

Modeling a domain: door mechanism

Let's move to the most intersting part - modeling.

Nothing gives so much adrenaline like modeling, isn't it?

Let's start with possible actions and states that are possible in our little area of activity.

Just so you know, from now on I am going to use "commands", instead of actions.

type DoorMechanismState = Closed | Opened | Locked

type DoorMechanismCommand = Open | Close | Lock | Unlock

type DoorMechanism = Mealy<DoorMechanismCommand, DoorMechanismState>

Simple, clean, understandable - F#.

We have our basic building concepts that work inside our domain.

Here is our recursive function we talked about:

let rec private continueAs (doorMechanism: DoorMechanismState): DoorMechanism =
    Mealy(fun doorMachineCommand ->
        match doorMechanism, doorMachineCommand with
        | Closed, Open -> ContinueWith(Opened, continueAs Opened)
        | Opened, Close -> ContinueWith(Closed, continueAs Closed)
        | Closed, Lock -> ContinueWith(Locked, continueAs Locked)
        | Locked, Unlock -> ContinueWith(Closed, continueAs Closed)
        | _, _ -> ContinueWith(doorMechanism, continueAs doorMechanism)
//  this is external "output" ____/              \___ here recursion happens!
    )

The most interesting part here is that this function (continueAs) creates a function, that accepts a doorMachineCommand as input (which actually is input for our state machine), and gets "packaged" into a Mealy type.

Inside, we are modeling all rules and transitions.

As you can see, dear Reader, our little door mechanism is not yielding Stop.

In this tiny tale, our state machine will "never terminate".

Right now, we can't yet use our state machine.

Let's fix it by defining a Send function

type Send<'Command, 'State> =
    'Command -> Mealy<'Command, 'State> -> Step<'State, Mealy<'Command, 'State>>

This function takes a command and a Mealy state machine and returns a Step.

Provided that state machine returned ContinueWith case, Step is going to keep a continuation function that will enable further state machine "evolution".

Let's implement it.

let send: Send<DoorMechanismCommand, DoorMechanismState> =
        fun doorMachineCommand (Mealy runDoorMechanismWith) -> 
            runDoorMechanismWith doorMachineCommand

It's not the most advanced piece of the code.

"Unwrapping" a Mealy machine in order to "run" our door mechanism with a given command.

We're almost there.

We somehow need to create a new door mechanism, right?

let create () = continueAs Closed

Running Mealy door mechanism

Let's create a simple mechanism:

let doorMechanism = DoorMechanism.create()

FSI shows the following result (on my local):

val doorMechanism: DoorMechanism = Mealy <fun:continueAs@23>

Woah, perfect encapsulation!

Ok, let's make it moving by sending Open to it:

doorMechanism
|> DoorMechanism.send Open

In return, this gave:

val it:
  StateMachines.Mealy.Step<DoorMechanismState,
                           StateMachines.Mealy.Mealy<DoorMechanismCommand,
                                                     DoorMechanismState>> =
  ContinueWith (Opened, Mealy <fun:continueAs@23>)

That's interesting, isn't it?

We got a Step that can be continued and it yielded Opened state of a state machine and...

...A continuation!

As it's opened, let's try to close it.

doorMechanism
|> DoorMechanism.send Open
|> DoorMechanism.send Close // ❌ bzzzzt, compile-time error!

Oops, something isn't working correctly.

Shouldn't we be able to send another command?

Well, yes.

But we didn't get a Mealy state machine back!

We have information that a state machine can continue processing. What's more, we also got a pair of current state and state machine continuation.

Could we just pattern match on ContinueWith and continue processing?

Well, not really.

We might eventually get Step and then we won't get a continuation back.

Hey, we are doing serious functional programming here!

What would you say, dear Reader, if we pass a function into Step, instead of "getting a state machine" out of the step?

One could say that we "bind" a function to a given Step, so this Step will have the responsibility to run this function inside.

Let's then define bind function:

let bind f (step: Step<'State, Mealy<'Command,'State>>) =
    match step with
    | Stop -> Stop
    | ContinueWith continueWith -> f continueWith

bind takes a function and a Step and provided that this Step can be continued, it applies a function to a continuation (yet another function).

So let's utilize it and fix compile-time error:

doorMechanism
|> DoorMechanism.send Open
|> bind (snd >> DoorMechanism.send Close) // ✅ works!

As a result we get:

val it:
  StateMachines.Mealy.Step<DoorMechanismState,
                           StateMachines.Mealy.Mealy<DoorMechanismCommand,
                                                     DoorMechanismState>> =
  ContinueWith (Closed, Mealy <fun:continueAs@23-1>)

As expected, our door mechanism is closed.

As you probably noticed, dear Reader, we used snd function that takes the second item from a pair.

That's because the result of send is a pair - current state machine state and "state machine itself" (in fact it's a continuation function but let's say it's a state machine).

So we just "discard" the current state, as we are not using it anywhere.

An avid Reader might correlate "bind" verb with Haskell community and well-known >>= operator.

Our language, F#, is so powerful that we can define such operator that will enable smoother usage:

let (>>=) step f = bind f step

Yup, that's it - we are reordering the arguments.

And finally, the usage:

let discardOutput = snd

doorMechanism
|> DoorMechanism.send Open
>>= (discardOutput >> DoorMechanism.send Close)
>>= (discardOutput >> DoorMechanism.send Lock)
>>= (discardOutput >> DoorMechanism.send Open)

Our final output is as follows:

val it:
  StateMachines.Mealy.Step<DoorMechanismState,
                           StateMachines.Mealy.Mealy<DoorMechanismCommand,
                                                     DoorMechanismState>> =
  ContinueWith (Locked, Mealy <fun:continueAs@23-1>)

I added an alias discardOutput for snd so that it communicates the intention (actually, that's the most important principle in software design!)

How functional are we?

Tired?

I hope not.

We have things to explore!

Let's use our Func-o-meter and check how functional we are!

How many functional points will we get?!

Showing how much our Mealy implementation is functional

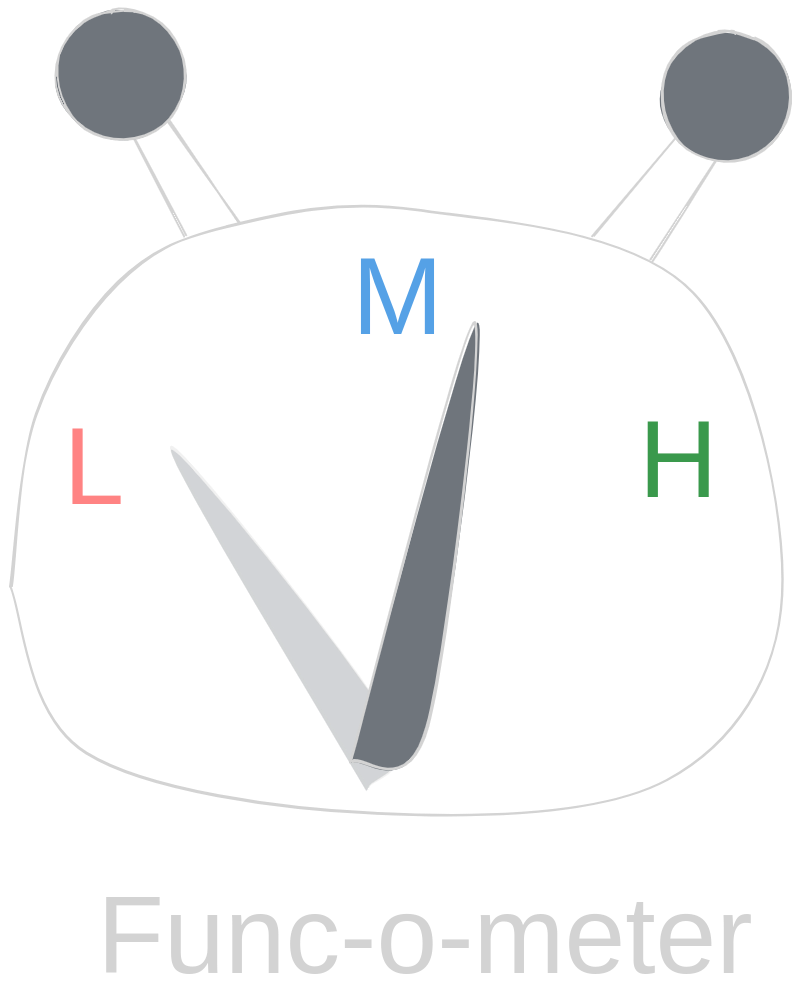
That's just fantastic!

Mealy state machine implementation beats Functional, State Machine-like approach!

Hurray!

Steady, gradual progress!

It's much more functional - we utilized recursion, pattern matching, we encoded invariants what does it mean "to stop a running state machine".

That's the engineering we are looking for!

Strange, I thought it will be close to High.

Can we be more functional?

Solution #2: Domain-specific language for defining state machines

Previous solution for sure is functional but is it readable?

Could we do a litmus test and show it to any "door mechanisms" expert and ask if we modelled it correctly?

Well, recursion does not help, for sure.

Maybe we should revisit our problem that we are trying to provide a solution for.

Let's bring the rules we started with:

• door mechanism starts as Closed
• only when it's Closed, when trying to Open it, it becomes Opened
• only when it's Opened, when trying to Close it, it becomes Closed
• only when it's Closed, when trying to Lock it, it becomes Locked
• only when it's Locked, when trying to Unlock it, it becomes Closed

I really believe that modelling "around" the language has superpowers included in it.

Ubiquitous language should live not only in spoken language, in models in our heads, but also in the code.

Ideally, we should be able to translate those rules into a specification on how the door mechanism works.

By using pseudocode, we could achieve something like this:

door mechanism:
    starts as Closed
    on Closed when trying to Open then becomes Closed
    on Opened when trying to Close then becomes Opened
    on Closed when trying to Lock then becomes Locked
    on Locked when trying to Unlock then becomes Closed

It's very readable, even non-technical experts will be able to comprehend it.

Also, it's very declarative - we state what happens and all "hows" are hidden, "abstracted away".

All the words we have used in our specification - they form a domain-specific language (DSL).

If we call it a ubiquitous language or domain-specific language - those are just labels for the same concept - efficient communication and smoother collaboration.

Ok, enough talking, let's build such declarative DSL in F#!

We are going to employ very powerful feature of F# - Computation Expressions (or CEs, shortly).

Computation Expressions empower us to create domain-specific languages, e.g.:

• Farmer for expressing Infrastructure as Code (IaC)
• Fun.Build for expressing CI/CD build scripts (and pipelines)
• sharp-point for building presentations
• and more!

It sounds like a perfect match - we want to express a specific language, coming from our tiny toy domain.

Expressing state machine

Yet again, let's remind ourselves main words (types) used in our "door mechanism area":

type DoorState = Closed | Opened | Locked
type DoorCommand = Open | Close | Lock | Unlock

We know what are the core concepts.

Our first specification, we want to implement, is creating a state machine that starts in a certain state:

let machine = stateMachine "doorMechanism" {
    startsAs Closed
}

We have the following words to cover:

• stateMachine
• startsAs

stateMachine is actual computation expression, whereas startAs is a custom operator within this computation expression.

Let's define the following core building blocks for our DSL:

type HandleCommand<'State, 'Command> = 'Command -> 'State

It simply represents a something that we're going to call a command handler.

Let's now add low-level contexts that will constitue our state machine:

type StateMachineContext<'State, 'Command when 'Command : comparison and 'State : comparison> =
{
    State: 'State
    Transitions: Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>
}

It should be self explanatory - it's a context with current state and map of all defined transitions.

Transitions are modeled as Map of possible states that lead to Map of commands, leading to functions for handling commands.

I think being "low-level" here will express the details (not the intentions) might be interesting to see that "there's no magic" (the only magical thing in this tale is our Func-o-meter, remember about it dear Reader).

And finally our state machine, that will be created from specification (we are wishing to build):

and StateMachine<'State, 'Command when 'Command : comparison and 'State : comparison> = StateMachine of stateMachine: StateMachineContext<'State, 'Command>

Now we are ready to roll out the implementation for stateMachine computation expression:

type StateMachineAssembler<'State, 'Command when 'Command : comparison and 'State : comparison>(name: string) =
    member this.Yield(_) = StateMachine { CurrentState = Unchecked.defaultof<_>; Transitions = Map.empty } 

    // 👇🏻 more members will come!

Our state machine assembler accepts a name, but it isn't used anywhere.

Then we have a first method, that are "natively" supported (and in some cases required) - Yield.

It helps returning a value from the computation expression.

This partical overloading of Yield says that given any argument, it's going to yield a broken state machine.

Why broken?

The fact we used Unchecked.defaultof<_> which does not look functional, and safe.

"Functional" might mean predictive, readable, safe and explicit.

Are we really dealing with StateMachine? Or maybe it's something different?

Of course, it turns out that we got a hint from our computation expression - in our lingo, the operation of building a state machine can be named as "assembling a state machine".

This pesky and implicit Unchecked.defaultof<_> (which in fact will manifest as dreaded null) expresses a concept which is missing in our code but for sure lives in the area of our problem.

Let's make it explicit!

type NotAssembledStateMachineContext<'State, 'Command when 'Command : comparison and 'State : comparison> =
{
    CurrentState: 'State option
    Transitions: Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>
}
and NotAssembledMachine<'State, 'Command when 'Command : comparison and 'State : comparison> = NotAssembledMachine of stateMachine: NotAssembledStateMachineContext<'State, 'Command>

Let's introduce NotAssembledMachine concept as type - it will be available only when specifying and assembling a state machine.

The external world should deal with StateMachine - which is ready to function (pun intended) and provide value to our consumers!

type StateMachineAssembler<'State, 'Command when 'Command : comparison and 'State : comparison>(name: string) =
        member this.Yield(_) = NotAssembledMachine { CurrentState = None; Transitions = Map.empty } 

Sounds like we are both having fun and modeling the domain of our tiny problem - neat!

Defining initial state

It's time for our first custom operator: startsAs:

type StateMachineAssembler<'State, 'Command when 'Command : comparison and 'State : comparison>(name: string) =
    // previous methods
    
    [<CustomOperation "startsAs">]
    member  this.startsAs ((NotAssembledMachine machine): NotAssembledMachine<'State, 'Command>, state: 'State) : NotAssembledMachine<'State, 'Command> =
        NotAssembledMachine { machine with CurrentState = Some state }

Looks quite simple - it accepts "previously" yielded/returned not assembled machine and makes it current state defined.

In fact - that the only requirement we have for each machine - it won't be able to do anything but at least it does no harm.

Now let's assemble our machine!

Turning not assembled machine into assembled one

type StateMachineAssembler<'State, 'Command when 'Command : comparison and 'State : comparison>(name: string) =
    // previous method
    member this.Run((NotAssembledMachine machine): NotAssembledMachine<'State, 'Command>) =
        match machine.CurrentState with
        | None -> failwith "You need to provide initial state for a state machine using `startsAs` operator."
        | Some state -> StateMachine { CurrentState = state; Transitions = machine.Transitions }

We used another "native" and built-in operator - Run - it executes a computation expression and the type returned from this method is exactly what consumers are getting.

So we need to be careful and provide working state machine!

As you can see, dear Reader, we check if CurrentState is available.

Eventually, we should get correctly assembled StateMachine (or runtime exception, in case we didn't cover initial state).

Let's create "an instance" of state machine assembler:

let stateMachine<'State, 'Command when 'Command : comparison and 'State : comparison> (name: string)  =
    StateMachineAssembler<'State, 'Command>  name

When we use our specification:

let machine = stateMachine "doorMechanism" {
    startsAs Closed
}

Everything compiles correctly!

Hurray!

Then, let's see what FSI tells us, when we "run" our machine assembler:

val machine: StateMachine<DoorState,DoorCommand> =
    StateMachine { CurrentState = Closed
                   Transitions = map [] }

Handling state transitions

Our machine works but not works.

We are able to assemble it, require it to start in certain state aaaand that's it.

We need specification of state transitions!

Now, we are going to add new computation expression - states that will accept more computation expressions!

Our goal is to provide states description in the given form:

let machine = stateMachine "doorMechanism" {
    startsAs Closed
    states {
        on Closed {
            whenTryingTo Open (thenBecomes Opened)
        }
    }
}

As you can see, dear Reader, we introduced the following concepts: states, on, whenTryingTo and thenBecomes.

Let's start with on computation expression.

Yet again, we need to have to have a "context" that will be evolving, as someone is going to use on computation expression.

Here's its type definition:

and StateTransitions<'State, 'Command when 'Command : comparison and 'State : comparison> =
{
    OnState: 'State
    Transitions: Map<'Command, HandleCommand<'State, 'Command>>
}

on computation expression is represented by StateTransitionsBuilder and looks as follows:

type StateTransitionsBuilder<'State, 'Command when 'Command : comparison and 'State : comparison>(fromState: 'State) =
    member _.Yield _ = Map.empty
    
    [<CustomOperation "whenTryingTo">]
    member _.whenTryingTo (ctx: Map<'Command, HandleCommand<'State, 'Command>>, command: 'Command, handleCommand:  HandleCommand<'State, 'Command>): Map<'Command, HandleCommand<'State, 'Command>> =
        ctx |> Map.add command handleCommand
    
    member this.Run(ctx: Map<'Command, HandleCommand<'State, 'Command>>): StateTransitions<'State, 'Command> =
        { OnState = fromState; Transitions = ctx }

It looks pretty similar to our StateMachineAssembler.

What's worth noticing is that we are able to capture specific concepts through custom operators - as we saw just before.

We define whenTryingTo operator - it basically adds a new handle command function by a command to a map of all command handlers Map.

Eventually, we return StateTransitions for a particular state.

Now, we can define on:

let on<'State, 'Command when 'Command : comparison and 'State : comparison> state =
    StateTransitionsBuilder<'State, 'Command> state

Also, let's define a helper function that nicely captures the language:

let thenBecomes nextState command  = nextState

It's dumb simple - just takes the state and returns it.

Time to check if our state transitions specification compiles!

let onClosedTransitions = on Closed {
    whenTryingTo Open (thenBecomes Opened)
}

All green, we are good!

Let's define the last computation expression that will appear in this tiny tale - states

Expressing all state transitions

Now we were dealing with transitions for a single state.

Time to handle all state transitions!

We're going to start with a builder:

type StateMachineStateTransitionsBuilder'<'State, 'Command when 'Command : comparison and 'State : comparison>() =
    member _.Yield(()) = ()

Nothing fancy - just a "default" Yield that actually will forbid using states computation expression without any state transitions.

Let's add another Yield, but this time for single state transitions:

type StateMachineStateTransitionsBuilder'<'State, 'Command when 'Command : comparison and 'State : comparison>() =
    // previous methods

    member _.Yield(stateTransitions: StateTransitions<'State, 'Command>) =
            Map.ofArray [| stateTransitions.OnState, stateTransitions.Transitions |]

Quite verbose.

Let's move on.

We know that each our state transitions specification might have many different possible state transitions.

Then we need to handle "multiple" values being yielded when specying our state machine.

type StateMachineStateTransitionsBuilder'<'State, 'Command when 'Command : comparison and 'State : comparison>() =
    // previous methods

    member _.Delay(f: unit -> Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>) = f()
    member _.Combine(newTransitions: Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>, previousTransitions: Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>) =
            newTransitions |> Map.fold (fun acc key value -> Map.add key value acc) previousTransitions
    member x.For(transitions: Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>, f: unit -> Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>) =
            x.Combine(transitions, f())

Yet again, we need to define three "native" methods - Delay, Combine and For.

I omit describing them for brevity.

The most important part is the intention behind it - we are merging all incoming transitions for a single state into a map of such descriptions.

Eventually, we need to Run our builder to return a value from computation expression:

type StateMachineStateTransitionsBuilder'<'State, 'Command when 'Command : comparison and 'State : comparison>() =
        // previous methods
        member x.Run(transitions: Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>) = transitions 

Time to define states!

let states<'State, 'Command when 'Command : comparison and 'State : comparison> =
    StateMachineStateTransitionsBuilder<'State, 'Command>()

Finally!

Let's use our newly created DSL to assemble a state machine!

(Yet again) Assembling a state machine

WHAT?!

A compile-time error? How could this be?!

let machine = stateMachine "doorMechanism" {
    startsAs Closed // ❌ bzzzzt, compile-time error!
    states {
        on Closed {
            whenTryingTo Open (thenBecomes Opened)
        }
    }
}

Inspecting the error message, one could see:

This control construct may only be used if the computation expression builder defines a 'For' method

Hmmm, it actually makes sense.

Our state machine assembler can handle only single value that gets yielded.

Each expression within computation expression returns something - if we put more expressions, we need to handle all the values.

Ok, let's come back to our StateMachineAssembler and provide methods for handling multiple values being return from expressions, inside of a computation expression.

type StateMachineAssembler<'State, 'Command when 'Command : comparison and 'State : comparison>(name: string) =
        // previous methods
            
        member this.Yield((transitions): Map<'State, Map<'Command, HandleCommand<'State, 'Command>>>) =
            NotAssembledMachine { CurrentState = None; Transitions = transitions }
        
        member this.Delay(f: unit -> NotAssembledMachine<'State, 'Command>) = f()
        member this.For((NotAssembledMachine machine): NotAssembledMachine<'State, 'Command>, f: unit -> NotAssembledMachine<'State, 'Command>) =
            this.Combine(NotAssembledMachine machine, f())
        member this.Combine((NotAssembledMachine newMachine): NotAssembledMachine<'State, 'Command>, (NotAssembledMachine existingMachine): NotAssembledMachine<'State, 'Command>) =
            let newTransitions =
                newMachine.Transitions
                |> Map.fold (fun acc key value -> Map.add key value acc) existingMachine.Transitions
            
            NotAssembledMachine { CurrentState =  newMachine.CurrentState; Transitions = newTransitions  }

It's pretty similar to what we saw in StateMachineStateTransitionsBuilder, when creating states computation expression.

All those methods are required to deal with many values.

What is worth noticing is the implementation of Combine:

// ...rest of computation expression
member this.Combine((NotAssembledMachine newMachine): NotAssembledMachine<'State, 'Command>, (NotAssembledMachine existingMachine): NotAssembledMachine<'State, 'Command>) =
    let newTransitions =
        newMachine.Transitions
        |> Map.fold (fun acc key value -> Map.add key value acc) existingMachine.Transitions
// ...rest of computation expression

It takes two not assembled machines and combines their state transitions - literally it merges them.

After handling all the methods, required to support multiple values returned from expressions, it's all green!

let machine = stateMachine "doorMechanism" {
    startsAs Closed // ✅ compiles!
    states {
        on Closed {
            whenTryingTo Open (thenBecomes Opened)
        }
    }
}

Final State Machine!

We are ready to express, using our DSL, the rules of a door mechanism:

• door mechanism starts as Closed
• only when it's Closed, when trying to Open it, it becomes Opened
• only when it's Opened, when trying to Close it, it becomes Closed
• only when it's Closed, when trying to Lock it, it becomes Locked
• only when it's Locked, when trying to Unlock it, it becomes Closed

let machine = stateMachine "doorMechanism" {
    startsAs Closed
    states {
        on Closed {
            whenTryingTo Open (thenBecomes Opened)
            whenTryingTo Lock (thenBecomes Locked)
        } 
        on Opened {
            whenTryingTo Close (thenBecomes Closed)
        }
        on Locked {
            whenTryingTo Unlock (thenBecomes Closed)
        }
    }
}

And it all compiles!

It sounds very natural!

It is very explicit!

F# in its purest form ❤️

LET'S RUN OUR STATE MACHINE!

val machine: StateMachine<DoorState,DoorCommand> =
    StateMachine
      { CurrentState = Closed
        Transitions =
         map
           [(Closed,
             map [(Open, <fun:machine@86-32>); (Lock, <fun:machine@87-33>)]);
            (Opened, map [(Close, <fun:machine@90-34>)]);
            (Locked, map [(Unlock, <fun:machine@93-35>)])] }

Specification of how our state machine works.

Isn't it beautiful?

But wait, we are not done yet.

We actually need to execute this specification!

As in the Solution #1: Mealy State Machines, we are going to define Send action:

type Send<'State, 'Command when 'State : comparison and 'Command : comparison> =
    'Command -> StateMachine<'State, 'Command> -> StateMachine<'State, 'Command>

Pretty straightforward.

Now implementation of a send function:

let send: Send<DoorState, DoorCommand> =
        fun command (StateMachine fsm) ->
            let newState =
                match fsm.Transitions |> Map.tryFind fsm.CurrentState with
                | Some transitions ->
                    match transitions |> Map.tryFind command with
                    | Some transition -> transition command
                    | None -> fsm.CurrentState
                | None -> fsm.CurrentState
            
            StateMachine { fsm with CurrentState = newState }

This function takes a command and finds all specified transitions for a current state, subsequently trying to find a command handler for a given command.

In case it was found - it applies a transition function to the command (in our tiny tale it's just returning a new state), else it remains in the same state.

Are you ready?

This is the final of the all finals!

Let's send some commands to our door mechanism state machine:

let machine' =
    machine
    |> send Open
    |> send Close
    |> send Lock
    |> send Open

FSI quickly gives us feedback:

  val machine': StateMachine<DoorState,DoorCommand> =
    StateMachine
      { CurrentState = Locked
        Transitions =
         map
           [(Closed,
             map [(Open, <fun:machine@86-22>); (Lock, <fun:machine@87-23>)]);
            (Opened, map [(Close, <fun:machine@90-24>)]);
            (Locked, map [(Unlock, <fun:machine@93-25>)])] }

As expected, we can't open a locked door mechanism!

Also, we clearly can see all transitions that need to be interpreted (which we already did!), but it nice to have it in a quite readable form.

How functional are we?

Wait!

We need to measure how functional is our DSL approach to create and run state machines!

Let's me pull Func-o-meter and check it.

Showing how much our DSL implementation is functional

CAN YOU BELIEVE THAT?!

We attained functional enlightment, and our work is a masterpiece.

DSL-based state machine specification beats everything in the world (in our tiny world of this tiny tale, but still).

Are you feeling boosted?

Empowered?!

WHAT THE HELL JUST HAPPENED?!

Well, we experienced and encountered maaaany things, along our journey.

We defined the domain of our problem and we tried to provide as functional solutions as possible.

We used helpful device called Func-o-meter to measure how functional solutions are:

• Mealy State Machines
• Domain-specific language for defining state machines

Unfortunately, I need to disappoint you, dear and patient Reader...

...Func-o-meter does not exist.

I must appologize you - I can't measure how functional the code is.

What does it really mean?

Recently, more and more languages are getting functional flavors (I am not calling them features, purposefully).

And that's good - but its worth keeping that in mind they might be "flavors", add-ins - not core concepts in which the language was forged.

Nothing wrong with that!

The language is a tool, and of course it shapes the way one is thinking, modeling and reasoning - still, the most important thing is delivering value to our users/customers, with software (or without it, actually).

So all the comparisons and measurements our imaginary Func-o-meter did, are farfetched.

Still we could define some tenets or attributes, that are attracted by functional-first thinking.

As I concluded in Many faces of DDD Aggregates in F#

And we were able to see this phenomenon, while experiencing our tiny journey.

Another one I would add to "functional-first thinking" basket is composition - on all levels - function composition, type composition.

Both immutability and composition, in my mind, express the most fundamental part of functional-first thinking - transformative nature.

Processes have a transformative nature too.

They make one thing become another and we literally saw that, especially in our lovely DSL.

Of course, we don't need to model everything in such a way - there's The cost of modeling for each model we build.

But I believe functional-first thinking helps us to perform modeling on the "highest" possible level - "becoming" level (you don't know what I am talking about? you might be interested in Modeling Maturity Levels).

So what I would suggest is to think in the "functional-first" way (immutability, composition and "transformatively") and not to "be" functional.

Closing

Thank you for your patience, dear Reader.

I hope you found it interesting to see the same problem from many different perspectives and to model the solutions on various levels.

One thing that is so important and it would be a shame for me if I didn't mention it.

We played with the powerful, functional-first language that F# is, but still the most important aspect of our job is understanding the problem we need to solve.

This reminds me the following saying:

As always, there's half truth, half "myth", but it gives the impression that we really need to be careful how we define our problems.

I feel it's a nice moment to stop our little journey, dear Reader.

Thank you and see you soon!

NOTE: source code will be shared soon